La Matrice Cellulaire : une architecture nouvelle

pour la nano-informatique

Auteurs: L.J.K. Durbeck and N.J. Macias

Traducteur: Aurélien Sagnier

Traduction partielleⁱ

traduction de Durbeck L and Macias N 2001 The Cell Matrix: an architecture for nanocomputing Nanotechnology 12 pp 217-30 (Bristol, UK: Institute of Physics Publishing) Copyright© 2001 Institute of Physics

Résumé

Récemment, d’importants efforts ont été consacrés au développement d’interrupteurs à l’échelle atomique et à la construction d’ordinateurs à partir de composants à l’échelle atomique. Nous proposons la construction de matériel informatique physiquement homogène et non différencié qui est différencié par la suite, après fabrication, en circuits numériques spécifiques. Ce procédé atteint deux buts simultanément en utilisant un même procédé de fabrication: le premier, immédiat, d’obtenir un ordinateur spécifique basé sur une unité centrale et une architecture de mémoire basée sur des interrupteurs à l’échelle atomique, ainsi que le second, plus général, qu’est la capacité de construire n’importe quel circuit numérique. De plus, ce procédé ouvre la perspective de mise en oeuvre fondamentale de circuits imprimés avec des caractéristiques dynamiques, massivement parallèles et automodifiables. En outre, l’architecture spécifique décrite dans ce document n’est pas particulièrement plus complexe que la plupart des autres architectures existantes, ce qui la rend plus facile à réaliser. Nous avons développé une architecture informatique appelée la Matrice Cellulaire qui tient davantage compte des contraintes de construction, ainsi qu’un procédé permettant de différencier du matériel informatique en circuit spécifique désiré de façon efficace et peu coûteuse. La Matrice Cellulaire est basée sur un élément atomique unique appelé cellule, qui, répliqué maintes fois, forme une matrice de cellules. En plus d’être d’application générale, cette architecture est hautement extensible, à tel point qu’elle semblerait donner accès à la différentiation et à l’utilisation de trillions de trillions d’interrupteurs. Cela n’est pas possible avec une architecture de réseau prédiffusé programmable par l’utilisateur, car leur réseau de portes est configuré en série, et la configuration en série de trillions de trillions d’interrupteurs prendrait des années. Cet article décrit la cellule en détail, ainsi que la façon dont les réseaux de cellules à l’intérieur d’une matrice peuvent être utilisés pour créer de petits circuits. Cet article décrit également un exemple d’application de cette architecture qui tire le meilleur parti d’un plus grand nombre d’interrupteurs.

Introduction

L’architecture décrite dans cet article est une plate-forme de calcul universelle qui permet de concevoir et de réaliser de façon fine des circuits numériques : son nom est la Matrice Cellulaire. Cette architecture sert à un mode de calcul du type un problème, une machine, dans lequel l’algorithme et l’ensemble des circuits sont conçus simultanément dès le départ, à un niveau aussi fin que la porte logique, si on le souhaite. Contrairement à d’autres architectures, celle-ci ne nécessite pas la construction d’un nano-assembleur (sur le modèle créé par Forrest Bishop en 1996) pour élaborer le modèle de calcul décrit ci-dessous, car la structure physique du matériel informatique est totalement fixe. Il s’agit d’une rangée de circuits de calcul dont la fonction est déterminée par la mémoire reconfigurable qui lui est incorporée. Grâce à cela, le matériel est « reconfigurable » selon le problème qu’il a à résoudre, tout comme les FPGA (Field Programmable Gate Array, réseau prédiffusé programmable par l’utilisateur). La structure physique de la Matrice Cellulaire présente l’avantage d’être non seulement fixe, mais de plus entièrement homogène, ce qui n’est pas le cas des autres matériels reconfigurables. En effet, son architecture s’appuie sur une structure unique dupliquée, appelée cellule, afin d’accomplir toutes les fonctions nécessaires, y compris la capacité de reconfigurer le matériel. A l’inverse des FPGA et des matériels utilisant un processeur et de la mémoire, la Matrice Cellulaire fonctionne sans superstructure ni structure spécialisée, mais uniquement grâce à des cellules identiques. La cellule est une structure simple, constituée de moins de 100 octets de mémoire et de quelques douzaines de portes logiques, ainsi que de fils la reliant aux cellules voisines (la conception de ces cellules et des matrices de cellules est décrite dans cet article). En conséquence, à partir du moment où les ressources existent pour construire une cellule structurellement simple et pour la connecter aux cellules voisines, il est possible de créer ou de développer une matrice entière par le biais d’une application répétée. La matrice peut alors être utilisée pour construire n’importe quel type de circuit numérique ou de composants comme des réalisations spécifiques de processeurs ou de mémoire, des processeurs parallèles, des multiprocesseurs, et bien d’autres composants encore.

Il y a des similitudes entre la Matrice Cellulaire et l’automate cellulaire créé par von Neumann en 1966 : ces deux structures sont composées de cellules identiques, connectées entre elles de façon rigoureusement analogue. Dans les deux, le comportement de la cellule dépend de son état ainsi que de celui des cellules voisines au moment de l’ordre. Cependant, si une Matrice Cellulaire tridimensionnelle est considérée comme un automate cellulaire, chacune de ces cellules dispose de 6,36 x 10²³⁴ états, soit 2^(768+12) car la table de vérité est constituée de 768 bits (table qui est indépendante de celle des cellules voisines), et les entrées de la cellule représentent 12 bits. Etant donné que chaque cellule possède six cellules voisines, le tableau de transition total d’un tel automate cellulaire contient 4,21 x 10¹⁵⁴³ entrées. De plus, le procédé de programmation de la Matrice Cellulaire est très proche de celui d’un circuit numérique de conception standard, et il a peu de point commun avec celui d’un automate cellulaire. En conséquence, il serait certainement plus naturel de considérer la Matrice Cellulaire non pas comme un automate cellulaire avec une table de transition fixe, mais plutôt comme un matériel à grain fin reconfigurable semblable à un FPGA, mais possédant des caractéristiques uniques dépassant celles d’un FPGA courant.

En plus de proposer une structure physique simple sur laquelle des systèmes de calcul complexes peuvent être créés, l’architecture de la Matrice Cellulaire fournit des solutions pour utiliser de façon efficace de grands nombres d’interrupteurs, car le niveau de complexité du système de commande est indépendant du nombre d’interrupteurs ; au contraire, le contrôle sur le système augmente avec le nombre de cellules. La commande de cette architecture à grain fin est interne et distribuée, ce qui permet à l’utilisateur de répartir un problème donné de façon temporelle, et non spatiale. Cette capacité s’applique particulièrement aux problèmes lourds mais naturellement parallèles comme une recherche portant sur une grande surface (par exemple dans le cas d’une détection de signature chimique, notamment pour détecter un cancer) qui décrypte du texte et cherche la racine de l’expression mathématique f (x) = n. Dans une machine traditionnelle, ces problèmes sont répartis de façon temporelle, car les éléments de l’espace dans laquelle la recherche est conduite sont analysés un par un jusqu’à ce que la réponse soit trouvée. En revanche, dans l’algorithme d’une machine à répartition spatiale, le processus de recherche dans les éléments peut être répliqué sur une grande matrice de processeurs qui effectuent chacun la recherche uniquement dans la portion de l’espace global qui leur a été attribuée. L’ensemble des processeurs peut alors opérer en parallèle, ce qui réduit le temps de recherche au temps nécessaire à un processeur pour accomplir sa charge de travail.

Cet article démontre qu’il est possible de construire un algorithme et une machine afin de répartir efficacement un problème de recherche entre un grand nombre de processeurs adaptés (voir ci-dessous) et de déchiffrer un cryptage à 56 bits. Cet article montre également que tous les processeurs nécessaires peuvent être construits en parallèle sur une Matrice Cellulaire. Ceci est important, car dans un FPGA contrôlé de façon externe, même si la machine fonctionne efficacement, la configuration, qui se ferait nécessairement en série, prendrait des mois, voire des années. En conséquence, l’architecture de la Matrice Cellulaire est actuellement la seule sur le marché à donner la possibilité de contrôler efficacement la construction et l’utilisation de systèmes qui tirent le meilleur parti en terme d’efficacité du très grand nombre d’interrupteurs que l’industrie de l’échelle atomique est en mesure de proposer.

Description

La réduction de la taille des systèmes fait partie des résultats les plus attendus des recherches de l’industrie de l’échelle atomique ; toutefois, ce sont les recherches portant sur la possibilité de construire des systèmes utilisant un nombre de composants plusieurs fois supérieur à ce qui était fait par le passé qui crée le plus d’effervescence. Ce développement, qui est vraiment remarquable, appelle nécessairement des innovations au niveau des architectures de calcul, et en particulier en ce qui concerne les structures et les processus de contrôle. Ces derniers doivent être développés de façon à ce qu’un nombre extrêmement important de composants puisse opérer efficacement en simultané.

C’est sur ce besoin d’ architectures de calcul innovantes que nous nous penchons ici. Les possibilités offertes par les architectures traditionnelles vont montrer leurs limites bien avant que les capacités de la construction à l’échelle atomique ne soient entièrement exploitées. Lors d’une conférence sur les architectures informatiques animée par Carver Mead en 2000, on lui demanda pourquoi la barre du calcul en parallèle à l’échelle de millions de processeurs n’avait pas encore était franchie. Il répondit en substance qu’ils avaient délibérément choisi de suivre une approche scalaire et que le plus gros et le seul obstacle vers le calcul parallèle à grande échelle était le succès même du calcul saclaire. Il est clair que les architectures actuelles (composées d’un processeur et de mémoire) vont tirer profit d’une plus grande densité car elles seront miniaturisées, ce qui diminuera le temps de réponse et ouvrira la voie à des systèmes plus puissants qui tiendront sur des ordinateurs plus petits. Elles bénéficieront également d’une augmentation du nombre d’interrupteurs dans une certaine mesure, car tous les composants systèmes, que ce soit l’unité centrale, la mémoire dure, la mémoire d’accès rapide, les coprocesseurs ou l’UAL, pourront être insérés dans le même substrat, ce qui réduira le temps de réponse. De même, la place ainsi libérée permettra d’ajouter de nouvelles fonctions système avancées pour les coprocesseurs et les UAL, ainsi que davantage de supports de langue ou d’instructions ; on pourrait même revenir à des jeux d’instruction d’un type identique à ceux utilisés avant le jeu d’instructions RISC (comme par exemple ceux du VAX 11/780). Cependant, l’impact sur les architectures traditionnelles risque de se limiter à ces évolutions-là et de ne pouvoir tirer entièrement parti du nombre extrêmement grand d’interrupteurs que la production à l’échelle atomique devrait atteindre, car il est particulièrement compliqué de faire évoluer de façon massive ce type d’architecture.

On peut affirmer sans se tromper que le processeur Pentium va atteindre ses limites ; en revanche, la solution pourrait se trouver dans un plus grand nombre de Pentiums. En effet, des ordinateurs multiprocesseurs très spécialisés sont en développement, comme le projet de 1999 d’IBM appelé « Blue Gene ». Malgré cela, les ordinateurs multiprocesseurs commerciaux souffrent généralement de goulots d’étranglements inter-processeurs, et à ce jour il n’existe pas de schéma de communication qui puisse gérer un million ou un milliard de processeurs pour ce type d’ordinateur. Certains chercheurs, notamment Mike Joy en 1992, se sont déjà penchés sur la nécessité d’avoir recours à des nouvelles méthodes et de nouvelles structures afin de contrôler des ordinateurs aussi puissants et complexes ; cependant nous n’avons connaissance d’aucune réalisation concrète autre que celle présentée ici. Il paraît évident que le degré de contrôle doit évoluer en même temps que le système informatique pour que la taille de ce dernier ne devienne pas une gêne. En générale, l’hypothèse selon laquelle un nombre n de processeurs utilisés pour une tâche donnée l’accomplira n fois plus vite qu’un seul processeur se révèle fausse (à de très rares exceptions prés), et ce car le temps système nécessaire pour coordonner l’utilisation d’un grand nombre de processeurs est beaucoup trop important.

Schéma peut affirmer sans se tromper que le processeur Pentium va atteindre 1. (a) Réseau de nœuds de calculs simples. Le schéma de connexion des nœuds n’est pas fixe, comme l’illustre l’image (b).

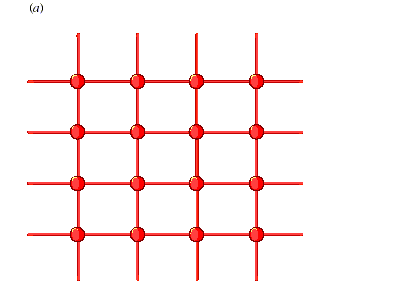
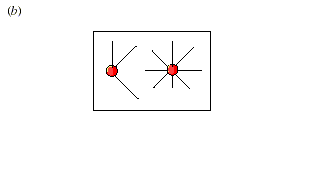
Cependant, il est possible d’obtenir une accélération multipliée par n pour n processeurs utilisés dans deux cas : si chaque processeur est choisi de façon appropriée (comme dans le projet « Blue Gene » d’IBM), ou si chaque processeur est configuré de façon appropriée, comme dans la Matrice Cellulaire.

Nos études appellent d’autres travaux : elles se rangent donc du côté de la demande de la nano-informatique et non de l’offre. Nous croyons que des interrupteurs à l’échelle atomique vont bientôt être produits (cf. les études de Collier et de ses assistants en 1999). Les questions auxquelles nous tentons d’apporter une réponse sont les suivantes : une fois obtenus des interrupteurs à l’échelle atomique, comment les organiser ? Et comment les utiliser pour obtenir des nano-ordinateurs ? Nous travaillons à la fois sur l’organisation physique (la structure), et l’organisation d’exécution (la fonction) des plate-formes de nano-informatique.

A) Organisation des nanostructures

1) Les Cellules

Notre architecture se fonde sur des éléments de calcul reconfigurables à grain extrêmement fin appelés « cellules », dans une topologie d’interconnexion simple. La conception de la cellule est simple et uniforme à travers toute la matrice. La complexité informatique vient de l’opération suivante, la programmation des cellules, et non pas de leur définition en tant que matériel. La Matrice Cellulaire peut être définie comme un réseau de nœuds dans lequel chaque nœud est un élément du circuit comme une porte ET, un additionneur complet 1 bit ou une longueur de fil. Ce concept est illustré par le schéma 1. Les FPGA peuvent également être modélisés de façon similaire ; toutefois, les grandes différences entre ces deux systèmes se situent au niveau des propriétés physiques et de la conception de l’architecture. La topologie de réseau est fixe et uniforme dans l’intégralité du système, mais lors de la production d’une Matrice Cellulaire, il est possible de créer une grande variété de topologies de ce type : les nœuds peuvent être connectés à 3, 4, 5 ou davantage de nœuds.

Schéma 2. Cellule dont le bloc mémoire est agrandi et montré en haut du schéma. La mémoire de la cellule est paramétrée pour réaliser un additionneur complet 1 bit. Cette cellule en mode D additionne A, B, et C_in et produit Σ_out et C_out. Les lignes fléchées indiquent des fils qui la connectent à une cellule voisine. Les cellules sont connectées à leurs voisins immédiats (ici, à quatre voisins). Le calcul est optimisé grâce au partage d’information entre cellules voisines, en parallèle.

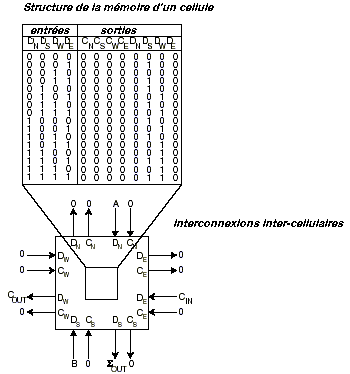
Les nœuds voisins sont généralement soit immédiatement adjacents, soit juste à côté, de façon à obtenir la structure la plus localisée et la plus simple possible. Le réseau est bidirectionnel, ce qui permet l’échange d’information en parallèle entre les nœuds. Le mot “ cellule ” réfère à l’unité physique dont est composée la Matrice Cellulaire. Les nœuds d’un réseau correspondent aux cellules individuelles, et le réseau lui-même aux interconnexions entre les cellules. Chaque cellule a la capacité d’accomplir des fonctions logiques simples à ses entrées ainsi que de produire une sortie. Parmi les fonctions logiques qui peuvent être utilisées, on compte les opérateurs utilisés traditionnellement pour l’intégration à petite échelle comme NON ET, OU exclusif, etc, mais également des fonctions plus complexes et plus avancées, comme un additionneur complet 1 bit, un multiplexeur, etc. En fait, une seule cellule à quatre côtés est capable de réaliser plus de 10¹⁹ fonctions différentes à partir de ses quatre entrées, et une cellule à six côtés peut réaliser plus de 10¹¹⁵ fonctions. Une partie de chaque cellule est attribuée à la mémoire : elle est utilisée pour spécifier sa fonction logique. Ce bloc de mémoire fonctionne comme le code machine d’une unité centrale, c’est à dire qu’il dicte à la cellule l’intégralité de la réponse aux entrées. Le schéma 2 illustre une organisation possible pour le bloc mémoire afin que la cellule accomplisse des opérations efficaces. Dans le cas présenté, la cellule est configurée en additionneur complet 1 bit : les cellules agissent alors comme des blocs logiques simples. Les fonctions plus complexes se construisent grâce à des amas de cellules. Une région d’une Matrice Cellulaire est ainsi configurée pour agir comme un circuit spécifique, c’est à dire que le bloc mémoire de chaque cellule est configuré pour accomplir un sous-ensemble d’un circuit plus grand.

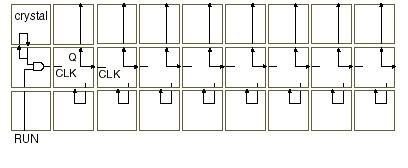
Schéma 3. Circuit simple construit sur un ensemble de 27 cellules de Matrice Cellulaire à quatre côtés. Ce circuit est un compteur. Les fils d’interconnexion entre les cellules ne sont pas représentés.

Chaque cellule est un nœud qui est une petite partie d’un grand système ou circuit. Le schéma 3 montre un exemple élémentaire d’un groupe de cellules qui sont programmées pour implémenter un compteur. La cellule dans le coin en haut à gauche est configurée pour agir comme un quartz : elle produit un modèle de bits hauts (ayant pour valeur 1) et de bits bas (ayant pour valeur 0). Les huit colonnes à droite sont huit bascules, composées de trois cellules chacune. L’entrée d’horloge est située sur la gauche de la cellule du milieu et la valeur du bit sort à sa droite, ainsi qu’en haut de la cellule supérieure. Si l’entrée attribuée à la cellule en bas à gauche a pour valeur 1, les bits du quartz seront dirigés vers l’entrée d’horloge de la bascule la plus à gauche, ce qui fera varier sa valeur de sortie tous les deux tics. Sa valeur de sortie est également transmise à la bascule suivante qui basculera tous les quatre tics, et ainsi de suite. L’ensemble des sorties forme donc un compteur en cascade. Notez bien que lorsqu’un ensemble de cellules fonctionne sur un « mode combinatoire », elles opèrent de façon asynchrone, sans horloge prédéterminée : les valeurs de sortie changent dès que l’ensemble des circuits de la cellule répond aux nouvelles entrées. Les nouvelles sorties ainsi obtenues sont aussitôt transmises aux entrées des cellules voisines. Cependant, il est possible de synchroniser ces opérations en construisant des lignes d’horloges, ou en utilisant des cellules en « mode modification ». Les cellules en mode « modification » changent leur mémoire de configuration (ou tables de vérité) de façon synchrone avec une horloge système globale ; ces changements peuvent être contrôlés et utilisés pour générer des horloges locales, dont le quartz du schéma 3 constitue un exemple.

2) Configuration des cellules

Nous allons maintenant nous pencher sur la façon dont chaque cellule devient une partie spécifique d’un circuit : comment les blocs mémoires des cellules sont-ils constitués, comment sont-ils configurés ? Etant donné que toutes les fonctions sont présentes au niveau des cellules, ces dernières doivent nécessairement posséder la capacité de configurer/constituer le système ; c’est la cas dans la Matrice Cellulaire. Les cellules peuvent interpréter les informations entrantes de deux façons distinctes : lorsqu’une cellule répond aux entrées en se basant sur sa configuration cellulaire, elle opère sur le mode « combinatoire », ou mode de traitement de données, comme un bloc logique combinatoire. En revanche, il existe un autre mode appelé mode « modification », qui permet à la cellule de considérer les bits/informations entrants comme nouveau code pour son bloc mémoire. Une cellule passe en mode «  modification » et traite les informations en conséquence grâce à un échange simultané avec une cellule voisine. Lors de celui-ci, la cellule voisine communique une nouvelle table de vérité à la cellule qui est modifiée. La configuration d’une cellule est donc une opération purement locale, qui implique uniquement deux cellules : celle qui possède l’information du nouveau code, et celle qui est ciblée et vers laquelle va l’information. La conséquence du caractère purement local de cette configuration est la possibilité de voir plusieurs processus du même type se dérouler en même temps dans différentes parties de la matrice.

L’état d’une cellule, et donc son mode, est déterminé par la valeur de son entrée C : si les entrées de C sont toutes égales à 0, la cellule fonctionne en mode « combinatoire », et il traite les données de l’entrée D pour produire des sorties D et C. En revanche, si une des entrées de C est égale à 1, la cellule est en mode « modification ». Dans ce cas, à tous les côtés où C_in = 1, les entrées D sont soumises à un opérateur OU spécifique, et le signal composite est chargé dans la mémoire de configuration de la cellule. Ce chargement s’effectue lors du front montant de l’horloge du système ; lors du front descendant le bit de configuration qui doit être remplacé à l’opération suivante est présenté à la sortie D de la cellule (sur les côtés ou C_in = 1). Ainsi, en affichant une valeur sur une de ses sorties C, une cellule X peut faire passer sa cellule voisine Y en mode «  modification ». X peut ensuite lire la mémoire de configuration de Y pendant le front descendant de l’horloge du système, et X peut charger de nouvelles données de configuration (ou les mêmes) dans Y pendant le front montant suivant. Ainsi, X peut lire la mémoire de configuration de Y simplement en manipulant ses sorties C et D, entre autre sous la forme d’une lecture non destructive.

Dans le mode «  combinatoire », les entrées D sont ainsi traitées par la mémoire de configuration de la cellule, alors qu’en mode « modification », elles sont utilisées pour réécrire cette dernière. Notez bien que chaque cellule à l’intérieur de la matrice est capable de fonctionner en mode « combinatoire » ou en mode « modification » : son mode n’est pas prédéterminé, et il est purement fonction des entrées qu’elle reçoit des cellules voisines. Dans une application complexe typique, la Matrice Cellulaire contient certaines cellules qui traitent des données, et d’autres qui modifient et reconfigurent des cellules. En fait, le bon fonctionnement de l’ensemble du système exige une grande coopération, une bonne interaction et des échanges entre les modes « combinatoire » et « modification » à l’intérieur de la Matrice Cellulaire. Grâce à ce fonctionnement, il est possible non seulement de faire des calculs d’ordre général en utilisant un amas de cellules, mais également de faire lire et modifier les informations de configuration des cellules par d’autres cellules. Ceci induit des circuits dynamiques et auto-configurables dont la durée d’exécution peut être modifiée en se basant sur des évènements au niveau local.

3) Implémentation des cellules

Le fonctionnement détaillé décrit ci-dessus peut être représenté sous la forme d’un circuit digital simple : le schéma 4 illuste un circuit pour une cellule avec quatre voisins.

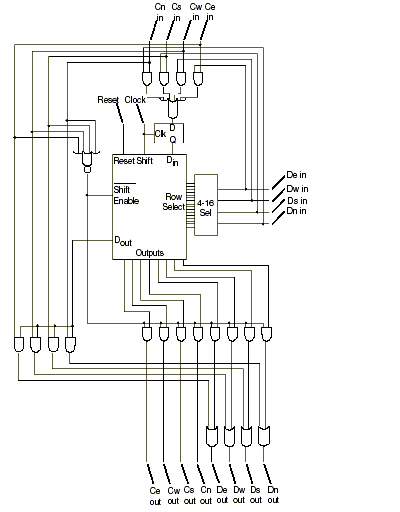
Schéma 4. Diagramme schématique de la spécification pour une cellule de la Matrice Cellulaire, montrant la logique numérique contenue dans une cellule.

Il y a plusieurs façons de concevoir et de construire une cellule, et à chacune correspondent des circuits numériques différents. Le schéma 4 illustre un type particulier de mise en oeuvre qui est décrit dans le brevet américain n° 5 886 537, mais d’autres designs plus simples ont également été brevetés (brevet américain n° 6 222 381). Dans ce schéma, les entrées C et D sont ici nommées fils d’entrée ou de sortie, mais ce sont les même que ceux illustrés dans le schéma 2 ; deux autres entrées sont également présentes. La légende « clock » correspond à l’horloge système qui est utilisée pour l’écriture et la lecture des informations de configuration depuis et à destination de la mémoire de configuration d’une cellule. « Reset » est utilisé pour programmer la mémoire de configuration de la cellule et lui donner un état prédéterminé, par exemple l’état dans lequel tous les bits de configuration sont égaux à 0 (instruction NOP). 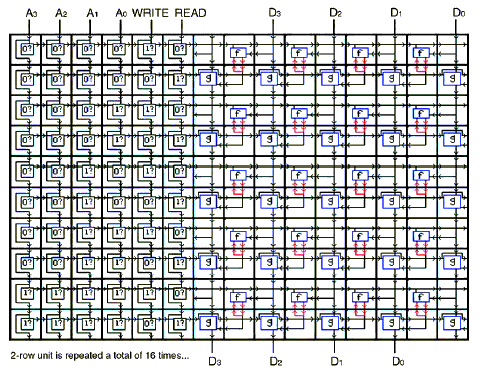Le bloc nommé
« 4-16 Sel » est un bloc logique séquentiel qui accepte quatre entrées et produit une affirmation à une de ses seize sorties en fonction du résultat. Le gros bloc au milieu du schéma 4 est la mémoire de configuration de la cellule ; elle est utilisée comme un registre à décalage. Les données sérielles sont introduites par l’entrée D_in, puis décalées lors du front descendant du décalage d’entrées. Un interrupteur à bascule verrouille un bit lors du front montant du signal de l’horloge, et celui-ci est présenté au registre à décalage de l’entrée D_in.

Schéma 5. Diagramme schématique d’une logique digitale contenue dans une mémoire 16 x 4 bits.

Le bit qui doit ensuite être décalé du registre est continuellement présenté à la sortie D_out. Le décalage est autorisé uniquement si la valeur de l’interrupteur permettant le décalage est égale à 1. Le registre à décalage est organisé non seulement en registre à décalage de 128 bits, mais encore comme une RAM de 16 x 8. Utilisée en tant que mémoire, une des 16 rangées est sélectionnée à travers/grâce à la valeur d’entrée du sélecteur de rangée. Les huit sorties sont transmises aux huit lignes de sortie qui apparaissent en bas du schéma. Pour être complet, il nous reste à préciser que l’entrée de réinitialisation donne une valeur prédéterminée à chacun des 128 bits constituant le registre à décalage. Aucune entrée ni sortie n’est mise en mémoire tampon au-delà de ce qui est montré dans le schéma 4. Par conséquent, le temps de production d’une sortie est strictement égal au temps nécessaire à l’ensemble des circuits pour répondre à un changement de valeur d’un entrée : dès que le contenu du registre à décalage est décalé ou que la valeur des entrées de D change, l’information est immédiatement traitée. Le verrouillage d’une partie des entrées par l’interrupteur à bascule et le décalage du registre à décalage sont les deux seules actions synchronisées par le signal de l’horloge. Veuillez noter que la structure d’une cellule est indépendante de la technologie de mise en oeuvre utilisée. Par exemple, dès que la « corde logique » décrite par Drexler (theorie du « rod logic », voir ses travaux de 1988) sera disponible, elle pourra être utilisée pour implémenter une cellule, au même titre que le silicium. A partir du moment où vous avez la capacité de construire une porte logique NON ET (NAND), des unités de mémoire (qui peuvent elles-mêmes être construites à partir de portes NON ET) et des interconnexions, vous pouvez construire une Matrice Cellulaire, indépendamment du type de technologie utilisée. Dans tous les cas, le composant qui prend le plus de place est le bloc mémoire qui contient les informations de configuration de la cellule. La taille de la mémoire est de 16 x 8 pour les cellules à quatre côtés, et de
64 x 12 pour les cellules à six côtés (qui peuvent être organisées physiquement en structures bidimensionnelles ou tridimensionnelles), ou de façon générale, de (2ⁿ) x (2n), où n représente le nombre de cellules voisines ou le nombre de côtés de la cellule. En plus de la mémoire, la Matrice Cellulaire contient quelques dizaines de portes simples (NON ET, OU, etc) ainsi que quelques multiplexeurs (ou sélecteurs) et des interrupteurs à bascule (mémoire à bit unique). La réalisation d’une cellule sur une puce en silicium nécessite environ 1000 transistors, dont plus de la moitié est allouée à la mémoire.

Schéma 6. Diagramme schématique du schéma 5 : une mémoire de 16 x 4 bits implémentée par les cellules d’une Matrice Cellulaire.

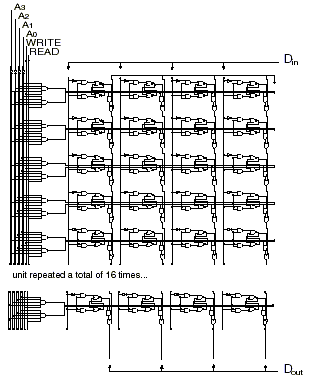
Nous avons déjà construit des petites matrices cellulaires sur des puces en silicium que nous avons utilisées pour de petits circuits. Actuellement, les techniques sur silicium permettent d’utiliser au moins 100 000 cellules, dans une configuration bidimensionnelle ou même tridimensionnelle. Cependant, afin de dépasser les performances des architectures et des circuits conventionnels et d’explorer la nouvelle frontière que les matrices cellulaires mettent à jour, il est indispensable que les techniques de fabrication évoluent de façon drastique en terme de densité par rapport à celles utilisées aujourd’hui sur le silicium.

De même, les recherches portant sur la fabrication pourraient également participer à ces objectifs en donnant accès à des amas cellulaires de taille plus importante au sein d’une matrice tridimensionnelle. En s’appuyant sur les estimations de Drexler (travaux de 1992) et de Freitas (travaux de 1999) et en comptant environ 500 portes par cellule et un trajet de propagation maximum de 10 portes entre entrée et sortie, on peut évaluer qu’une cellule d’une Matrice Cellulaire occuperait 8000 nm³, dissiperait 6,5 x  10^-21 J et pourrait basculer en 1 ns.